Xin chào 👋 Dạo gần đây, sự xuất hiện thường xuyên của các Mô hình sinh (Generative models) với các ứng dụng vô cùng thiết thực như Sinh văn bản (Text generation) hay Sinh hình ảnh từ văn bản (Text-2-Image). Cụ thể hơn, với Text generation, các mô hình ngôn ngữ lớn (Large language models) như GPT-3, GPT-4 của Open AI hay gần đây nhất LLaMA của Meta đang chiếm spotlight trên mọi bài báo, blogs về NLP. Còn với Text-2-Image, Midjourney, Imagen hay Stable diffusion là những cái tên không mấy xa lạ được nhắc nhiều khi nói về bài toán này.
Sự phát triển nhanh của mô hình sinh đòi hỏi chúng ta cần tìm hiểu và nắm bắt chúng để không bị “bỏ lại phía sau” với sự phát triển như vũ bảo này. Bài blog này sẽ nói về mô hình Variational Autoencoder (VAE) - một Generative model - được sử dụng trong bài toán Text-2-Image.
Autoencoder
Trước khi tìm hiểu về mô hình VAE, chúng ta sẽ nhắc về kiến trúc mô hình Autoencoder. Kiến trúc này bao gồm hai thành phần chính là Encoder và Decoder. Cụ thể, Encoder sẽ cố gắng biểu diễn dữ liệu đầu vào ở miền không gian ẩn (Latent space), ít chiều hơn so với không gian dữ liệu (Data space) ban đầu. Nói cách khác, dữ liệu đầu vào sẽ được nén lại bởi Encoder. Trong khi đó, Decoder có chức năng tái tạo lại dữ liệu đầu vào từ biểu diễn ở không gian ẩn. Hình ảnh bên dưới sẽ minh họa trực quan về kiến trúc này.
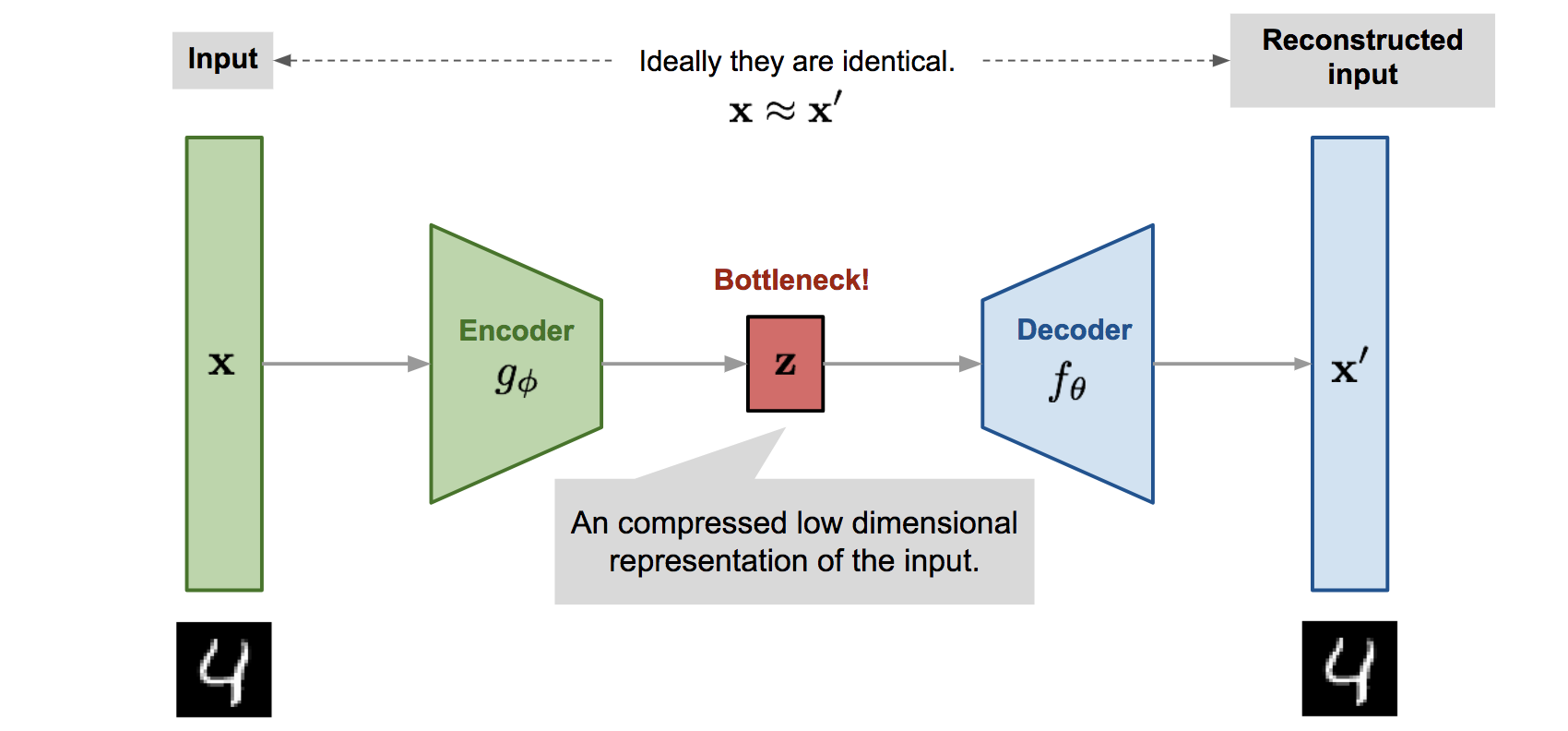Kiến trúc mô hình Autoencoder (Nguồn: Lil’Log)
Mô hình Autoencoder thường được sử dụng cho các bài toán như Khử nhiễu hình ảnh (Image Denoising), Phát hiện bất thường (Anomaly Detection) hay Phân đoạn hình ảnh (Image Segmentation). Vậy nó được sử dụng trong bài toán sinh ảnh như thế nào? Rõ ràng, khi không gian ẩn được xây dựng “tốt”, việc sinh ảnh có thể dễ dàng thực hiện bằng cách chọn một điểm ngẫu nhiên trong không gian đó và tiến hành “reconstruct”.
Không gian ẩn phải được chuẩn hóa (regularization) bằng cách thỏa mãn được hai tính chất sau:
- Tính hoàn chỉnh (Completeness): Mỗi điểm trong latent space sẽ tương ứng với một điểm có thật trong data space.
- Tính liên tục (Continuity): Các điểm gần nhau trong latent space sẽ có tính chất giống nhau trong data space.
Rõ ràng, latent space trong Autoencoder không thể thỏa mãn được hai tính chất này, khi mà encoder là hàm đồng nhất (Identity function).
Chuẩn hóa Latent space (Nguồn: Joshep’s blog)
Variational Autoencoder
Mô hình Variational Autoencoder (VAE) được đề xuất lần đầu bởi Diederik P Kingma vào năm 2013. Trong đó, Chữ Variational trong VAE có nguồn gốc từ phương pháp Variational inference (Xấp xỉ phân phối xác suất).
Khác với Autoencoder, VAE sẽ không cố gắng mapping dữ liệu đầu vào thành một vector cố định. Thay vào đó, VAE sẽ mapping thành một phân phối như hình minh họa bên dưới.
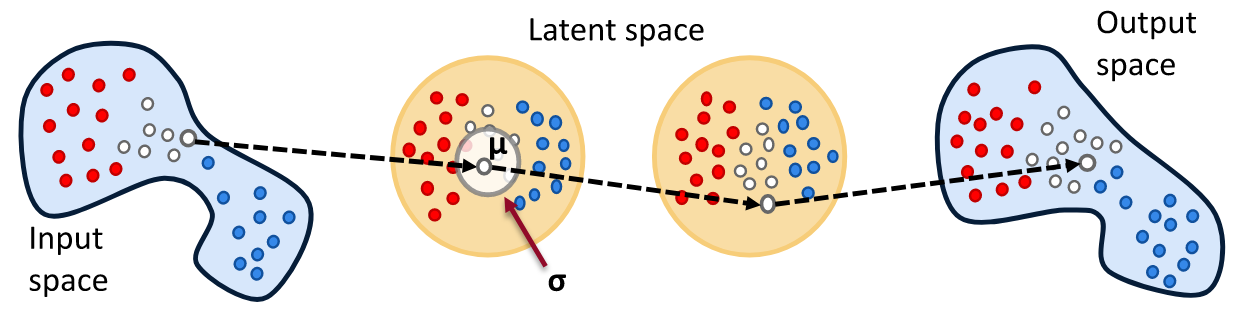Latent space của VAE (Nguồn: tvhahn)
Thế nhưng việc mapping thành phân phối xác suất vẫn không đảm bảo rằng latent space thỏa mãn được hai tính chất nêu trên. Do đó, chúng ta phải đồng thời chuẩn hóa cả mean và covariance matrix bằng cách “ép” phân phối này thành phân phối chuẩn (Gaussian distribution). Điều này làm covariance matrix gần bằng identity matrix và các phân phối không bị tách ra xa một cách vô nghĩa.
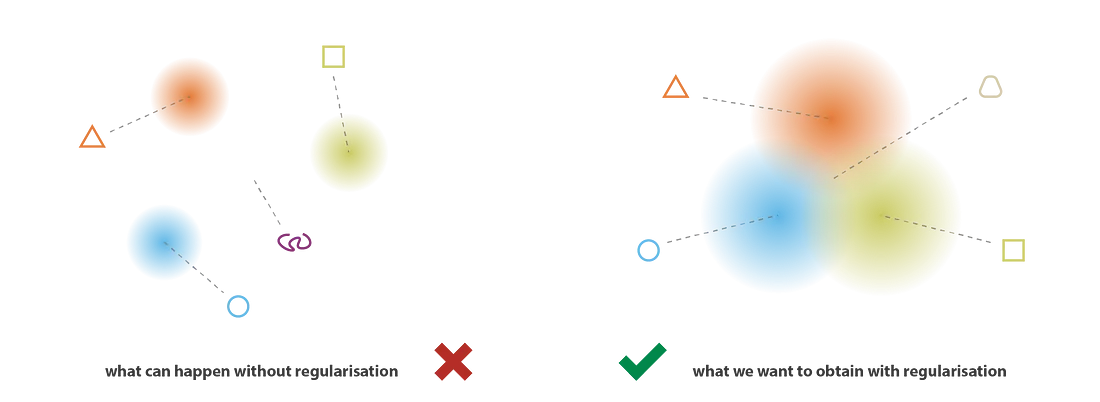Chuẩn hóa Latent space (Nguồn: Joshep’s blog)
Vậy chúng ta làm như thế nào? Trước tiên chúng ta cần mô hình hóa những gì cần thiết. Cụ thể hơn, ta gọi phân phối cần tìm là $p_\theta$, được tham số hóa bởi $\theta$, $x$ là dữ liệu đầu vào và $z$ là vector tương ứng của $x$ ở latent space.
Theo công thức Bayes, ta có: $p_\theta(z|x) = \frac{p_\theta(x|z)p_\theta(z)}{p_\theta(x)}$
- Prior probability $p_\theta(z)$: chúng ta sẽ giả định phân phối này tuân theo phân phối chuẩn.
- Likelihood $p_\theta(x|z)$: có thể dễ dàng tính tương tự như Autoencoder
- Posterior probability $p_\theta(z|x)$: không thể tính (intractable) khi việc tính toán $p_\theta(x) = \int p_\theta(x|z)p(z)dz$ là vô cùng khó khăn (tích phân trên không gian nhiều chiều). Do đó, thay vì cố gắng tính một cách trực tiếp, chúng ta sẽ xấp xỉ xác suất này bằng phương pháp Variational Inference.
Đặt $q_\phi(z|x)$ là phân phối xấp xỉ cần tìm, mục tiêu của chúng ta là $q_\phi(z|x) \approx p_\theta(z|x)$. Để làm được điều này, chúng ta sẽ sử dụng độ đo Kullback–Leibler divergence. Cụ thể, \(D_\text{KL}(X\|Y)\) sẽ đo lường lượng thông tin mất mát khi dùng phân phối $Y$ thể hiện cho phân phối $X$.
Trong bài toán này, chúng ta sẽ cố gắng cực tiểu hóa \(D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}) )\). Thế nhưng tại sao chúng ta lại sử dụng $D_\text{KL}(q_\phi | p_\theta)$ (Reverse KL) mà không phải \(D_\text{KL}(p_\theta \| q_\phi)\) (Forward KL)? Câu trả lời sẽ được tóm gọn như sau (bạn có thể tìm được câu trả lời một cách chi tiết trong blog này):
- Khi cực tiểu hóa Forward KL, chúng ta sẽ kéo dãn $Q(Z)$ để nó có thể che phủ được hết $P(Z)$.
- Ngược lại, khi cực tiểu hóa Reverse KL. $Q(Z)$ sẽ có xu hướng “co” lại dưới $P(Z)$.
- Cả hai đều có những đặc tính riêng, việc chọn lựa Forward KL hay Reverse KL phụ thuộc vào bài toán. Trong bài toán này, tính chất của Reverse KL phù hợp hơn.
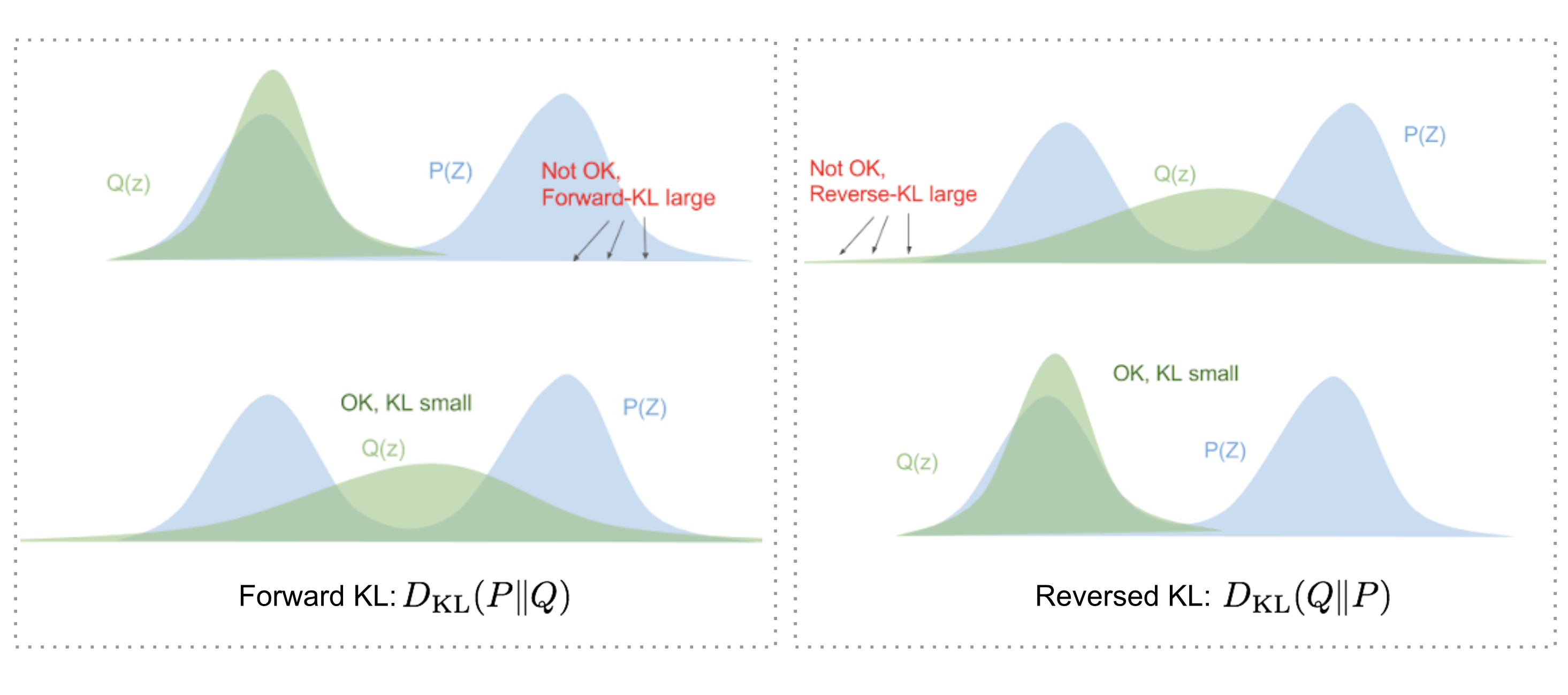Sự khác biệt giữa Forward KL và Reverse KL. Hàng bên trên thể hiện giá trị KL lớn, hàng bên dưới thể hiện giá trị KL nhỏ. (Nguồn: Eric Jang’s blog)
Chúng ta biết rằng mục tiêu của chúng ta là cực tiểu hóa \(D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}) )\). Thế nhưng, rõ ràng chúng ta không thể tính được $p_\theta(z|x)$, do đó cần phải biến hóa một tí:
\[\begin{aligned} & D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}) ) & \\ &=\int q_\phi(\mathbf{z} \vert \mathbf{x}) \log\frac{q_\phi(\mathbf{z} \vert \mathbf{x})}{p_\theta(\mathbf{z} \vert \mathbf{x})} d\mathbf{z} & \\ &=\int q_\phi(\mathbf{z} \vert \mathbf{x}) \log\frac{q_\phi(\mathbf{z} \vert \mathbf{x})p_\theta(\mathbf{x})}{p_\theta(\mathbf{z}, \mathbf{x})} d\mathbf{z} & \scriptstyle{\text{; Because }p(z \vert x) = p(z, x) / p(x)} \\ &=\int q_\phi(\mathbf{z} \vert \mathbf{x}) \big( \log p_\theta(\mathbf{x}) + \log\frac{q_\phi(\mathbf{z} \vert \mathbf{x})}{p_\theta(\mathbf{z}, \mathbf{x})} \big) d\mathbf{z} & \\ &=\log p_\theta(\mathbf{x}) + \int q_\phi(\mathbf{z} \vert \mathbf{x})\log\frac{q_\phi(\mathbf{z} \vert \mathbf{x})}{p_\theta(\mathbf{z}, \mathbf{x})} d\mathbf{z} & \scriptstyle{\text{; Because }\int q(z \vert x) dz = 1}\\ &=\log p_\theta(\mathbf{x}) + \int q_\phi(\mathbf{z} \vert \mathbf{x})\log\frac{q_\phi(\mathbf{z} \vert \mathbf{x})}{p_\theta(\mathbf{x}\vert\mathbf{z})p_\theta(\mathbf{z})} d\mathbf{z} & \scriptstyle{\text{; Because }p(z, x) = p(x \vert z) p(z)} \\ &=\log p_\theta(\mathbf{x}) + \mathbb{E}{\mathbf{z}\sim q\phi(\mathbf{z} \vert \mathbf{x})}[\log \frac{q_\phi(\mathbf{z} \vert \mathbf{x})}{p_\theta(\mathbf{z})} - \log p_\theta(\mathbf{x} \vert \mathbf{z})] &\\ &=\log p_\theta(\mathbf{x}) + D_\text{KL}(q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z})) - \mathbb{E}{\mathbf{z}\sim q\phi(\mathbf{z}\vert\mathbf{x})}\log p_\theta(\mathbf{x}\vert\mathbf{z}) \end{aligned}\]Rút gọn và biến đổi phương trình, ta được: \(\log p_\theta(\mathbf{x}) - D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}) ) = \mathbb{E}_{\mathbf{z}\sim q\phi(\mathbf{z}\vert\mathbf{x})}\log p_\theta(\mathbf{x}\vert\mathbf{z}) - D_\text{KL}(q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}))\)
Từ đây, chúng ta định nghĩa hàm lỗi như sau: \(\begin{aligned} L_\text{VAE}(\theta, \phi) &= -\log p_\theta(\mathbf{x}) + D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}) )\\ &= - \mathbb{E}_{\mathbf{z} \sim q\phi(\mathbf{z}\vert\mathbf{x})} \log p_\theta(\mathbf{x}\vert\mathbf{z}) + D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}) ) \\ \theta^{}, \phi^{} &= \arg\min_{\theta, \phi} L_\text{VAE} \end{aligned}\)
Hàm lỗi này được gọi là “Variational lower bound” hoặc “Evidence lower bound”. Trong đó, từ “lower bound” đến từ việc KL divergence luôn dương, dẫn đến $-L_\text{VAE}$ luôn bé hơn hoặc bằng $\log p_\theta (\mathbf{x})$. Do đó, việc cực tiểu hóa hàm lỗi $L_\text{VAE}$ tương đương với việc cực tiểu hóa \(D_\text{KL}(q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}))\) . Tóm lại, để tính được hàm lỗi, chúng ta cần tính được hai giá trị \(-\mathbb{E}_{\mathbf{z} \sim q_\phi(\mathbf{z}\vert\mathbf{x})} \log p_\theta(\mathbf{x}\vert\mathbf{z})\) và \(D_\text{KL}(q_(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}))\). Trong đó, giá trị thứ nhất gọi là “reconstruction loss” và có thể được tính bằng hàm lỗi tương đương Cross Entropy (bạn đọc có thể tham khảo chi tiết tại đây). Còn lại giá trị thứ hai chính là KL Divergence giữa đầu ra encoder và $\mathcal{N}(0, I)$.
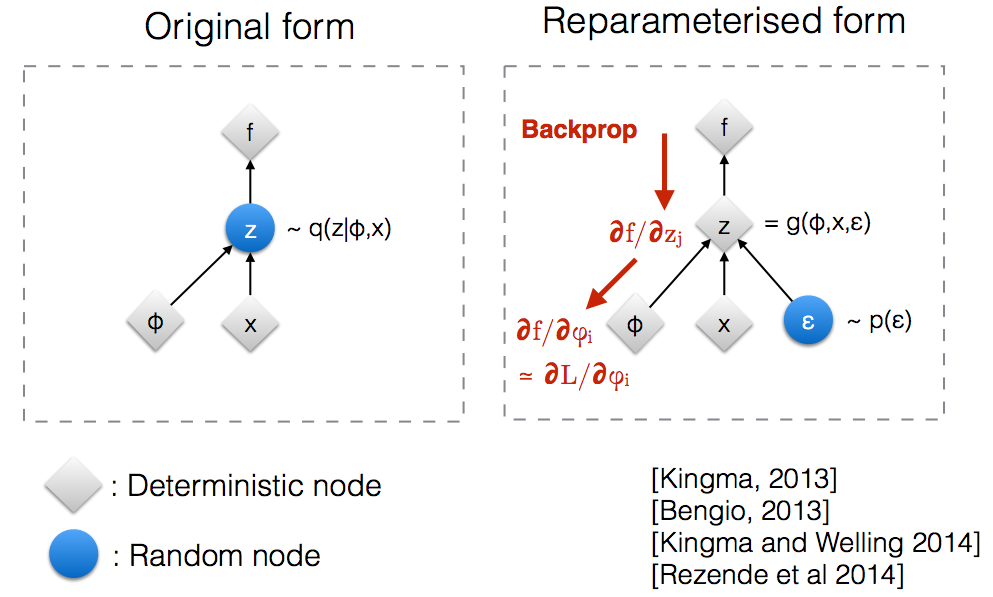
Trước khi kết thúc bài viết này, chúng ta sẽ xem xét qua một thứ gọi là “Reparameterization trick”. Làm sao để chúng ta có thể backpropagation với một quá trình ngẫu nhiên khi sampling $z \sim \mathcal{N}(\mu, \sigma^2)$? Thay vì chọn $z$ trực tiếp từ $\mathcal{N}(\mu, \sigma^2)$, chúng ta sẽ biểu diễn $z = g(\mu, \sigma, \epsilon)$. Trong đó, $g = \mu + \sigma\epsilon$ với $\epsilon \sim \mathcal{N}(0, I)$.
Reparameterization trick
Tổng Kết
Qua bài viết này, chúng ta đã cùng nhau nhìn lại về mô hình Autoencoder, sự khác nhau giữa Autoencoder và Variational Autoencoder. Bên cạnh đó, chúng ta cũng biết được thế nào là một latent space “tốt”, làm sao để xấp xỉ một phân phối, thế nào là ELBO loss và cuối cùng là Reparameterization trick. Mong rằng bài viết này sẽ có ích đến với mọi người 😽 Tạm biệt 👋🏻